131

QU’EST-CE, AU JUSTE,
QU’UNE PROBABILITÉ ?

De Laplace à Popper

Francis Bismans

Université de Lorraine, BETA Research Associate, Nelson Mandela Metropolitan University
Port Elizabeth (South Africa)

INTRODUCTION1

Disons-le d’emblée : on s’intéressera exclusivement, dans cet article, à la probabilité mathématique et à ses différentes interprétations. Bien sûr, il existe d’autres voies d’investigation du concept – philosophique par exemple, ce qui est la démarche empruntée par Cournot (1851, chapitre iv).

De même, il est possible d’aborder la probabilité dans sa relation avec le hasard – ici aussi Cournot (1851) constitue une bonne référence – ou encore avec la statistique mathématique. On peut aussi en faire une pièce essentielle de ce que plusieurs auteurs ont appelé la « querelle du déterminisme ».

Cependant, ce n’est pas le chemin qui sera ici suivi, puisque, répétons-le, seules les interprétations du concept mathématique seront prises en considération.

132

Pour autant, même ainsi délimité, le champ de la recherche reste très vaste. Certes, on concédera aisément que l’étude ne doive pas remonter jusqu’à Aristote. À proprement parler, l’origine du calcul des probabilités peut être datée de 1654 exactement, lorsque Pascal et Fermat s’échangèrent plusieurs lettres sur le problème des « partis » soulevé par le chevalier de Méré. Cependant, on aura beau parcourir ces lettres ou encore le traité « Des combinaisons » (Pascal 1665, p. 77-83), on n’y trouvera pas le terme de probabilité lui-même.

Après Pascal, plusieurs mathématiciens – le plus important d’entre eux est Huygens – continuèrent à étudier les jeux de hasard en utilisant l’outil créé par l’auteur des Pensées : la combinatoire. Parallèlement, tout au long du xviiie siècle, comme le signale Szafarz (1985), plusieurs savants, pas tous mathématiciens, ont produit des études démographiques et des tables de mortalité, qui ont permis de sortir du domaine étriqué et idéalisé des jeux de société.

Progressivement, l’expression de « chance » ou de « probabilité » en vint à désigner un nombre fractionnaire égal au nombre de cas favorables rapporté au nombre de cas possibles, sous la condition que ces derniers soient « équipossibles ». C’est ce concept qu’on désigne généralement sous le terme de « probabilité classique ». Un outil mathématique – l’analyse combinatoire – permet alors de mesurer, c’est-à-dire de compter, dénombrer les cas favorables et les cas possibles.

Toutefois, une telle définition, appropriée pour les jeux de hasard, n’était d’aucune utilité pour les praticiens ou démographes dont on vient de parler : comment en effet dénombrer les « cas possibles », lorsqu’on s’intéresse, par exemple, à la probabilité pour un homme de 40 ans de mourir dans les dix années à venir ? La probabilité pour ces praticiens est alors ce que l’on appelle en termes modernes, une fréquence relative : ici, l’occurrence du nombre de morts parmi les hommes de 40 ans durant la décennie future rapportée au nombre total de ces derniers.

C’est le mérite de Jacob (ou Jacques) Bernoulli d’avoir jeté un pont entre ces deux définitions en établissant une première forme de la loi dite des grands nombres – en fait, il s’agit de la « loi faible » démontrée dans le cas particulier d’un nombre fini d’essais, caractérisés chacun par deux résultats seulement.

Tout au long du siècle des Lumières, de nombreux auteurs – Moivre, Euler, D’Alembert, Lagrange, Buffon, Condorcet, pour n’en citer que 133quelques-uns – s’illustreront dans cette branche nouvelle du calcul des probabilités. Le nom de Bayes doit plus particulièrement être mis en avant, lui que l’on peut créditer, comme l’a montré Stigler (1986, p. 123-124), de l’introduction du concept de probabilité conditionnelle.

Néanmoins il faudra attendre Laplace et son imposante Théorie analytique des probabilités pour qu’advienne la grande synthèse qui dominera quasiment tout le dix-neuvième siècle. Schneider (1987, p. 190) parle même à ce sujet d’un « paradigme » pour tout le siècle et pose la question : pourquoi et comment se fait-il que « Laplace ait détenu une telle position dominante » – de surcroît, pendant une période aussi longue ? On ne tentera pas de répondre à cette interrogation. On se contentera simplement de relever que le rôle éminent joué par Laplace dans le développement du calcul des probabilités justifie pleinement de commencer notre enquête historique par cet auteur. (Si l’on considérait l’histoire de la statistique mathématique, il faudrait alors s’arcbouter sur la « synthèse de Gauss-Laplace » – l’expression est de Stigler [1986, chapitre 4].)

On laissera donc dans l’ombre la « préhistoire » de la synthèse laplacienne, en renvoyant tous ceux qui voudraient en savoir plus sur la question aux ouvrages fondamentaux de Hacking (1975) et de Daston (1988).

Pour autant, se donner un point de départ ne dit pas encore comment la matière elle-même doit être développée et exposée. À cet égard, on voudra bien nous concéder deux présupposés, dont il n’est pas difficile de démontrer le bien-fondé :

1. La formalisation de la théorie des probabilités va nécessairement de pair avec les progrès des mathématiques directement concernées – l’analyse en l’occurrence ; en d’autres termes, comment, par exemple, penser, au sens fort du terme, la loi de probabilité d’une variable aléatoire absolument continue sans utiliser l’intégrale de Riemann ou mieux, celle de Lebesgue ?

2. Il est commode de réduire les interprétations de la probabilité à deux grands ensembles : les conceptions subjective et objective. Bien sûr, cette distinction ne s’est pas imposée d’emblée, mais on peut considérer qu’elle devient dominante dans les années vingt à quarante du siècle précédent. Elle se révèle éclairante 134pour qui veut organiser des développements historiques diffus, fragmentés, porteurs d’allers et retours multiples, parsemés de ruptures et de contradictions.

Compte tenu de ces présupposés, l’article sera structuré comme suit. Une première section rendra compte de la synthèse opérée par Laplace. Elle montrera que chez cet auteur, même si la définition classique est dominante, il y avait aussi, au moins en germe, les premiers éléments d’une conception fréquentiste de la probabilité, qui sera alors systématisée et axiomatisée par Richard von Mises. La section deux est tout entière consacrée à l’examen du grand ouvrage de Keynes, le Treatise on Probability, ainsi qu’à l’étude de sa postérité, en la personne notamment de H. Jeffreys et J. Hicks. La section suivante, après avoir introduit la distinction poppérienne entre probabilités subjectives et objectives, s’attache à retracer plus particulièrement l’émergence de la première à partir de la séquence chronologique Ramsey-de Finetti-Savage. Elle en propose aussi une critique à partir du « paradoxe d’Allais ». La quatrième section décrit la « révolution théorique » opérée par Kolmogorov qui réalisa en 1933 une axiomatisation, féconde et durablement influente, de la théorie des probabilités. Dans la foulée, l’interprétation – néo-objectiviste et « propensionniste » – de Popper est présentée ; elle s’appuie en effet entièrement sur le formalisme de Kolmogorov. Une cinquième section est consacrée à la critique poppérienne du déterminisme scientifique et de la conception qui lui est liée, de la probabilité en tant que mesure de notre ignorance. Enfin, la dernière section conclut.

Un dernier mot, presque une excuse, avant de commencer : le fait que plusieurs économistes de talent, à commencer par Keynes, Allais et Hicks, aient joué un rôle notoire dans le développement des différentes interprétations de la probabilité, justifie amplement le léger biais « économiciste » qui transparaît de temps à autre dans cet article.

135

I. L’APPROCHE CLASSIQUE ET SES DÉVELOPPEMENTS

On énoncera la définition de la probabilité donnée par Laplace et on examinera ses liens avec l’interprétation fréquentiste. On verra ensuite les développements, les raffinements de l’approche laplacienne, associés au nom de Richard von Mises, qui conduisent en réalité à une définition nouvelle, formalisée, de la probabilité.

LA SYNTHÈSE DE LAPLACE

Pierre-Simon Laplace publia en 1812 sa Théorie analytique des probabilités et une deuxième édition deux ans plus tard – c’est cette dernière que l’on utilisera. Le livre contenait par ailleurs une introduction qui résumait sans recourir aux mathématiques la partie analytique de l’ouvrage. Cette introduction fera l’objet d’une publication séparée sous le titre Essai philosophique sur les probabilités. La première édition de l’Essai paraîtra en 1814 et la cinquième en 1825.

La construction laplacienne se présente comme une majestueuse cathédrale – si l’on ose dire. Elle regorge de résultats nouveaux et utilise le meilleur des mathématiques de l’époque. On y trouve par exemple une première démonstration du théorème de la limite centrée, dans le cas particulier certes, mais important, où l’on a affaire à une suite (infinie) d’essais bernoulliens. Surtout, les applications couvrent quasiment la totalité des phénomènes physiques, sociaux et humains : les jeux de hasard bien sûr, mais aussi la philosophie naturelle, la mécanique céleste, les sciences morales, les tables de mortalité, les jugements des tribunaux, les bénéfices des établissements, telles sont quelques-uns des sujets d’études préférés de Laplace. Notre auteur formule même le vœu qu’on « traite l’économie politique, comme on a traité la physique, par la voie de l’expérience et de l’analyse », donc par le calcul des probabilités – cité dans Laplace (1825, p. 277).

L’Essai débute par l’affirmation très nette du déterminisme laplacien. Très rapidement cependant, Laplace (1825, p. 35) présente sa définition – qui deviendra classique – de la probabilité : « La théorie des hasards consiste à réduire tous les événements du même genre à un certain nombre de cas également possibles (…) et à déterminer le nombre de 136cas favorables à l’événement dont on cherche la probabilité. Le rapport de ce nombre à celui de tous les cas possibles est la mesure de cette probabilité (…) ».

En se servant du formalisme moderne, on considère une expérience aléatoire définie par l’équipossibilité des résultats. L’univers desdits résultats est l’ensemble des cas possibles : Un événement A est un sous-ensemble de Ω constitué des m événements élémentaires où et 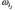désigne un cas favorable. La probabilité de A est alors le rapport :

(1)

où card X désigne le nombre d’éléments de X, ici de A ou de Ω.

Les limitations d’une telle définition sont évidentes. Elles concernent tout particulièrement la fameuse restriction d’équipossibilité des cas, qui revient en quelque sorte à supposer que ces cas sont tous également probables. Cette insuffisance – il y en a d’autres ! – rend la définition inadéquate pour traiter de nombreuses applications de la théorie des probabilités.

Toutefois, Laplace (1825, p. 78) faisait également référence dans son Essai au théorème de Bernoulli – une première version de la loi faible des grands nombres ainsi qu’on l’a indiqué. Ce dernier avait en effet prouvé dans son Ars Conjectandi que si on considère la suite de variables aléatoires indépendantes prenant la valeur 1 avec probabilité et la valeur 0 avec probabilité (1-), alors plus est grand et plus la fréquence relative, c’est-à-dire le nombre d’occurrences de 1 rapporté au nombre d’essais, est proche de .

Laplace généralise ce théorème sous deux aspects : d’une part, il prend en considération des variables aléatoires – pour utiliser un langage moderne2 – qui revêtent plus de deux valeurs ; d’autre part, il simplifie la démonstration en utilisant la méthode des fonctions génératrices. (Sur cette méthode, voir Laplace [1814, p. 80 et sq.] ; de nos jours, on 137peut donner une démonstration élémentaire de la loi faible des grands nombres en appliquant l’inégalité de Bienaymé-Tchebychev, comme par exemple dans Bismans [2016]).

Toujours est-il que la loi faible des grands nombres conduit presque automatiquement à assimiler probabilité classique et fréquence relative observée au cours d’une suite d’essais. On peut en conséquence créditer Laplace d’être véritablement le grand ancêtre de la probabilité « fréquentiste ».

Cela dit, l’évolution ultérieure de l’approche consistera à se débarrasser de la définition classique – de plus en plus perçue comme insuffisante – et à assimiler purement et simplement la probabilité à la valeur limite d’une fréquence relative sur une suite d’essais indéfiniment répétés. À cet égard, un nom doit être cité en premier lieu : Richard von Mises.

LA DÉFINITION FRÉQUENTISTE

Richard était le frère de l’économiste libéral Ludwig von Mises. Il fut reçu docteur de l’université de Vienne en 1908, où il avait étudié les mathématiques, la physique et les sciences de l’ingénieur. Il sera nommé professeur de mathématiques appliquées à l’université de Strasbourg l’année suivante tout en restant un membre actif du « Cercle de Vienne ».

Il est le premier à avoir présenté, en 1919, une axiomatisation de la probabilité – voir von Mises (1919, 1957, 1981). Notre auteur se donne comme objectif de traduire en termes mathématiques le point de vue selon lequel la probabilité est mesurée comme une fréquence relative sur une longue suite d’essais.

Pour ce faire, il introduit d’abord le concept de collectif (Kollektiv en allemand) : « Nous ne parlerons pas de probabilité tant qu’un collectif n’a pas été défini » (von Mises, 1957, p. 18). Informellement, un collectif est une suite d’observations d’un même événement qui satisfait deux axiomes : (i) la fréquence relative de l’occurrence de cet événement admet une limite (pour cette raison, on peut le nommer axiome de convergence) ; (ii) cette limite n’est pas modifiée lorsqu’on substitue à la suite initiale une sous-suite quelconque sélectionnée de manière appropriée.

Toute la difficulté de construction d’un collectif tient en fait dans la sélection des sous-suites en question. Von Mises – voir également 138Szafarz (1984) – a lui-même donné un exemple d’une suite qui satisfait le premier axiome, mais non le second. Le voici. Considérons une très longue route pourvue de bornes, de grande taille tous les kilomètres et de petite taille tous les cent mètres. Intéressons-nous ensuite à la fréquence relative de l’apparition des grandes bornes. La suite complète admet évidemment la limite 1/10. Par contre, la sous-suite constituée par la sélection d’une borne sur deux admet la limite 1/5. En conséquence, le second axiome est violé.

Pour sortir de cette difficulté, von Mises a précisé que la sélection des sous-suites devait s’opérer en supprimant des termes de la suite initiale exclusivement en fonction des termes antérieurs. Un exemple simple permet d’illustrer la procédure. Considérons la suite :

En conservant les deux premiers termes de cette suite et puis en sélectionnant un terme subséquent sur deux, on obtient la sous-suite 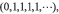qui satisfait le critère de sélection imposé.

Compte tenu de cette précision, on peut formellement réécrire comme suit l’axiomatique de von Mises. Soit un ensemble fini

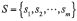
et l’application définie sur l’ensemble des entiers naturels hors le zéro et à valeurs dans S :

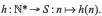
L’application est ensuite astreinte à suivre la propriété suivante : si on pose

(2)

où 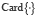désigne le cardinal de l’ensemble considéré,

alors

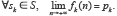(3)

Par conséquent, la probabilité 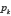est la limite de la fréquence relative de 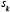parmi les premiers termes de la suite. L’axiome 1 de convergence est ainsi satisfait.

139

Pour que l’axiome 2 – on le qualifiera désormais d’axiome du hasard ou de stochasticité – soit également vérifié, il faut ajouter la condition supplémentaire que la propriété (3) doit être rencontrée pour toute sous-suite extraite en supprimant des termes de la suite initiale en fonction des seuls termes antérieurs.

De prime abord, il n’y a rien à redire a priori à cette formalisation, sauf qu’elle s’applique aussi à des suites qui n’ont rien de probabiliste ou qui sont parfaitement prédictibles. Toute la question réside en effet dans le choix de sous-suites réellement aléatoires – plus exactement « quasi-aléatoires », car l’on sait depuis pas mal de temps déjà que le hasard ne s’imite pas. C’est ce qu’affirmait déjà Borel (1939, p. 82), « il n’est pas possible à l’esprit humain d’imiter parfaitement le hasard, c’est-à-dire de substituer un mécanisme rationnel quelconque à la méthode empirique qui consiste à effectuer une suite indéfinie d’épreuves répétées, de parties de pile ou face par exemple ».

CRITIQUES DE LA CONCEPTION FRÉQUENTISTE

L’approche de von Mises est critiquable à deux points de vue au moins : sa cohérence interne d’une part ; son incapacité à traiter les probabilités d’événements « isolés », singuliers, d’autre part.

En ce qui concerne la première critique, plusieurs auteurs – Copeland et Wald, notamment – ont montré que l’axiome de stochasticité n’était pas cohérent (consistant) d’un point de vue logique. En bref, le problème réside – on l’a déjà effleuré – dans la construction de suites réellement aléatoires. Copeland et Wald ont ainsi démontré qu’il n’existe qu’un système dénombrable de règles de choix, ce qui contredit la propriété (3) qui doit être satisfaite chez von Mises pour toute sous-suite extraite en supprimant des termes en fonction des seuls termes initiaux retenus. On peut certes reformuler l’axiome en question de manière à le rendre logiquement cohérent, mais on perd alors la compréhension intuitive qui caractérisait la démarche première de von Mises. De plus, comme le souligne Breny (1975, p. 20), la théorie, même ainsi corrigée, est insuffisante pour décrire, par exemple, l’évolution d’une épidémie, au cours de laquelle la probabilité de contamination varie avec le temps.

La critique de Popper est plus générale encore. Celui-ci part essentiellement de l’approche de von Mises tout en rejetant ses deux axiomes 140de convergence et de stochasticité. La manière dont il s’y prend est fort technique. Disons simplement qu’il tente de reconstruire une théorie fréquentiste – Popper (1980, p. 154 et sq.) – qui reformule, « améliore » selon son expression, l’axiome de stochasticité et qui élimine complètement celui de convergence. Pour autant, notre auteur n’était pas lui-même convaincu du bien-fondé de sa reconstruction : Popper (1980, p. 147, note*1) signale, en effet, que depuis 1934 (date de la parution de la première édition allemande de la Forschung), il avait modifié de trois manières sa théorie de la probabilité : en particulier, affirmait-il,

j’ai remplacé l’interprétation objective de la probabilité en termes de fréquence par une autre interprétation objective – la « propensity interpretation » – et remplacé le calcul des fréquences par le formalisme néo-classique (ou de la théorie de la mesure).

L’objection la plus répandue à l’égard de la théorie fréquentiste est aisée à formuler : elle ne s’applique qu’à des événements répétés à l’identique et en conséquence, elle est inapte à rendre compte d’événements singuliers ou isolés – « uniques » pourrait-on dire. Un bon représentant de cette tendance critique – il en existe bien d’autres ! – est Savage (1954b), qui écrit : « d’un point de vue objectiviste, les probabilités ne peuvent s’appliquer fructueusement qu’à des événements répétitifs, c’est-à-dire à certains processus seulement ».

C’est Reichenbach (1937, p. 314 et sq.) – dans un gros article (plus de 80 pages !) qui est en fait un résumé de Reichenbach (1935) – qui, parmi les fréquentistes de l’époque, a tenté de réfuter le plus vigoureusement la critique émise à partir du « cas isolé ». Sa thèse est radicale : « Le terme “probable” admet toujours une interprétation dans le sens d’une fréquence, même si l’individu qui emploie le mot nous assure qu’il n’a pas pensé à une fréquence. C’est ce que j’appelle la “toute-puissance” de l’interprétation de la fréquence ». Et l’auteur de prendre l’exemple de la probabilité que Jules César ait visité l’Angleterre. Il s’agit évidemment d’un « cas isolé ». Cependant, l’historien qui s’attache à déterminer cette probabilité va inclure cet exemple dans la classe des événements semblables et en conséquence, c’est donc une statistique qui le conduit à la probabilité cherchée. Évidemment, il est facile de rétorquer que la classe en question est si peu fournie, que la notion de fréquence n’y a tout simplement plus aucun sens ! Certes, l’exemple choisi par Reichenbach n’est pas celui qui 141est le plus favorable à sa thèse. Il n’empêche que la cause nous paraît entendue et que le problème du fameux « cas isolé » ne peut, en général, être résolu adéquatement dans le cadre de la problématique fréquentiste.

Au total, il est donc légitime, c’est aussi l’opinion de Szafarz (1984), de parler d’échec, au moins relatif, de l’axiomatique misessienne tout en n’oubliant pas ses mérites et surtout, le fait qu’elle permettait de traiter, de manière satisfaisante, nombre de phénomènes aléatoires répétitifs !

I. LE PROBABLE COMME RELATION LOGIQUE

John Maynard Keynes est certes l’auteur de la General Theory, mais aussi d’un Treatise on Probability, paru en 1921, qui développe une interprétation originale connue sous le nom de « probabilité logique ».

LA RELATION DE PROBABILITÉ

Keynes se place d’emblée dans le sillage de Leibniz en reproduisant en exergue de son livre une citation – en vieux français ! – de ce dernier : « J’ai dit plus d’une fois qu’il faudrait une nouvelle espèce de logique, qui traiteroit des degrés de Probabilité ». Concevoir la théorie des probabilités comme une branche de la logique résume l’approche de l’économiste de Cambridge. Certes, il consacre tout un chapitre de son Treatise, le chapitre viii, à l’exposé et à la critique de la conception fréquentiste de la probabilité. Mais à cette interprétation (frequency theory), il substitue celle de la probabilité comme relation logique entre des propositions ou énoncés.

Son apport essentiel consiste, dans ses propres termes, « à discuter de la vérité et de la probabilité de propositions à la place de l’occurrence et de la probabilité d’événements » (Keynes, 1921, p. 5).

Si l’on dispose de prémisses constituées par un ensemble de propositions et d’une conclusion formée par un corps de propositions , on dira qu’il existe une relation de probabilité de degré entre et si implique au degré . Formellement, on peut noter, à la suite de Keynes, cette probabilité de la manière suivante :

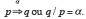(4)

142

La relation présente deux cas extrêmes : si peut être déduit de , alors et si est la contradictoire de , alors Tous les autres cas se situent entre ces deux opposés et peuvent recevoir une interprétation intuitive : la probabilité de la proposition (étant donné ) est d’autant plus proche de l’unité que le contenu de ajoute moins à celui de ou encore la probabilité de mesure le degré de vérité de contenu dans la proposition .

Puisque la probabilité mesure l’intensité de la confiance dans la relation logique entre deux propositions ou deux ensembles de propositions, elle a un côté essentiellement subjectif, variable en fonction de chaque individu amené à rendre un jugement de probabilité. C’est pour cette raison que Keynes (1921) parle d’un « degré de croyance », mais ce degré est rationnel (rational belief) : il n’est donc pas arbitraire, mais repose ou s’appuie sur la force du lien logique entre les propositions examinées. Keynes (1921, p. 4) admet le caractère subjectif de son approche, mais, ajoute-t-il, « une fois que les faits qui déterminent notre connaissance sont donnés, le probable ou l’improbable dans ces circonstances a été fixé objectivement ». (À vrai dire, cette argumentation n’est pas convaincante, car elle revient à réaffirmer la rationalité des degrés de croyance – sans plus.)

Au total, la probabilité est donc le degré de confiance rationnelle qu’une personne ou un individu peut accorder à la proposition q sur base de l’information contenue dans p.

Keynes peut alors utiliser la probabilité ainsi définie pour « logiciser symboliquement » dans la partie II du Treatise, les principaux théorèmes de la théorie des probabilités, un peu à la manière de Russel et de Whitehead qui dans leurs Principia Mathematica, avaient tenté de déduire la totalité des mathématiques de leur temps à partir d’un nombre réduit d’axiomes et de définitions.

Cette partie II a fait l’objet de plusieurs critiques. Ainsi Borel (1924, p. 135-136) dans sa recension du Treatise peut-il écrire que les mathématiciens n’éprouvent pas « le besoin de créer (…) des difficultés artificielles, en renonçant aux ressources de la langue vulgaire et en la remplaçant par un symbolisme hiéroglyphique ; ce symbolisme n’a jusqu’ici conduit à aucune découverte proprement mathématique ». Évidemment, cette appréciation sévère – trop sévère – de Borel s’explique par le « réalisme » que le grand mathématicien a toujours manifesté.

143

Parallèlement, plusieurs auteurs ont détecté des erreurs ou des déficiences dans l’écriture logique des énoncés de probabilité opérée par Keynes. Ainsi Braithwaite (1973, p. xvi-xvii), dans sa présentation éditoriale du Treatise publiée dans les Collected Writings de Keynes, tome 8, relève que « le développement axiomatique des théorèmes du calcul des probabilités présente de sérieux défauts formels ».

PROBABILITÉ ET MESURE

Il est difficile de donner une valeur numérique à la probabilité définie par Keynes. Comment en effet comparer des probabilités entre des propositions qui n’ont pas d’éléments communs ? Par exemple, comment pourrait-on évaluer les valeurs logiques des deux énoncés suivants : « le taux d’intérêt sera de 5 % étant donné telle forme de la courbe de préférence pour la liquidité » et « les nageurs ne parviendront pas jusqu’à la côte par suite de la présence de requins » ?

Keynes (1921, p. 21) en était bien conscient qui écrivait : « On a supposé jusqu’ici comme évident que la probabilité est, dans le sens plein et littéral du mot, mesurable. Je devrais limiter, non étendre la doctrine populaire ».

Plus précisément, notre auteur distingue parmi l’ensemble des degrés de croyance trois sous-ensembles (Keynes, 1921, p. 41-43) :

1. le sous-ensemble des probabilités numériques ;

2. le sous-ensemble des probabilités comparables ordinalement, mais non représentables numériquement ;

3. le sous-ensemble des probabilités non comparables.

Pour expliciter cette typologie, précisons que des probabilités sont comparables dans deux cas essentiellement : 1) lorsqu’on compare la probabilité de deux conclusions sur base d’une même donnée, soi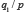t et 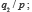2) quand on cherche l’influence d’un changement des données sur la vraisemblance d’une même conclusion, soit et Sur l’ensemble des propositions comparables, on peut alors définir une relation « est plus probable ou aussi probable que ». Cette relation « justifie les comparaisons de plus et de moins entre les probabilités qu’il est impossible de mesurer numériquement, théoriquement autant que pratiquement » (Keynes, 1921, p. 70). (En fait, cette dernière formulation est inexacte : 144Debreu, par exemple, a montré qu’une relation constituant un préordre total peut être représentée par une fonction continue, à valeurs réelles, sur l’ensemble préordonné par la relation considérée, moyennant une hypothèse additionnelle de continuité.)

À ce stade, la question surgit de savoir quand deux énoncés peuvent être considérés comme équiprobables. Pour répondre à cette question, Keynes introduit le principe d’indifférence, qui est un décalque de celui de raison insuffisante attribué à Bernoulli, à savoir : l’égalité entre deux probabilités n’a de sens que pour les énoncés de la forme 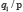et 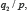c’est-à-dire pour des conclusions fondées sur une même donnée .

Dès lors, dans l’ensemble des probabilités comparables, seules pourront faire l’objet d’un calcul celles auxquelles on peut appliquer le principe d’indifférence.

Enfin, subsiste le vaste domaine des conclusions pour lesquelles la relation « plus ou aussi probable que » n’est pas applicable. Reste alors ce jugement de Keynes (1921, p. 41) : « il est toujours vrai de dire d’un degré de probabilité qu’il n’est pas identique soit avec l’impossibilité soit avec la certitude, qu’il se trouve entre les deux (…) ». En d’autres termes, tout ce que l’on peut affirmer, c’est que la probabilité en question se trouve « quelque part » entre le certain et l’impossible.

On pourrait montrer, mais la place manque pour le faire, que la non-mesurabilité de la probabilité et l’impossibilité corrélative d’un calcul prévisionnel fondé sur l’espérance mathématique, courent comme un fil rouge dans les analyses de la Théorie générale. Sans parler du fameux article du Quarterly Journal of Economics, dans lequel Keynes (1937, p. 114, 116) écrit explicitement : « (…) il n’y a pas de base scientifique pour former quelque probabilité calculable que ce soit. Nous ne savons tout simplement pas. (…) J’accuse la théorie classique (…) de traiter le présent en faisant abstraction du fait que nous savons très peu sur le futur. »

KEYNES ET SA POSTÉRITÉ

De Finetti (1985, p. 359, 362) a fait la remarque que la non-mesurabilité de la probabilité chez Keynes n’était pas adaptée au « développement de la théorie mathématique des probabilités » et qu’elle le plaçait de ce fait hors du courant dominant (mainstream). Indubitablement, le jugement de Finetti est correct. Il explique pourquoi l’ouvrage de l’économiste de Cambridge, malgré des comptes rendus globalement 145positifs, comme celui de Borel (1924), a été, dans une large mesure, ignoré par la postérité.

Il faut citer néanmoins parmi ceux qui se sont placés dans le sillage de Keynes, Harold Jeffreys, de Cambridge lui aussi, et John Hicks. La tentative du premier d’axiomatiser la logique du probable se veut – et est – plus rigoureuse que celle de Keynes. Sans entrer dans les détails, disons simplement qu’il considère à nouveau la probabilité comme un « degré de confiance », mais il adopte un système d’axiomes et de conventions qui lui permet de conclure à la mesurabilité de la probabilité. Dans ses propres termes (voir Jeffreys, 1939, 1948, p. 24), il obtient le résultat :

Théorème 8. Toute probabilité peut être exprimée par un nombre réel.

Là réside la différence essentielle entre les deux auteurs, qui partagent, pour le reste, une même approche logique de la relation de probabilité.

John Hicks (1979, p. 114), pour sa part, discute les axiomes de Jeffreys ; il substitue au premier d’entre eux la formulation suivante : sur base des données, soit la proposition A est plus probable que B, soit B est plus que probable que A, soit elles sont également probables, soit elles ne sont pas comparables. Dès lors, Hicks en revient explicitement au schéma de Keynes, rappelé plus haut, en distinguant trois classes parmi les degrés de croyance : les probabilités numériques, les probabilités comparables, mais non exprimables par un nombre, et enfin celles qui ne sont même pas comparables. Hicks (1979, p. 115 n. 19) adopte le diagramme de Venn suivant pour illustrer sa vision des trois classes probabilistes :

Fig. 1

146

A représente l’ensemble des probabilités numériques ; B celui des probabilités qui constituent un ordre (en fait, un préordre) et C celui des probabilités non comparables. Cependant, même dans ce dernier cas, Hicks maintient que des jugements de probabilité peuvent parfois être formulés.

De plus, le prix Nobel affirme également que le champ de l’économie proprement dite – sous l’angle de la probabilité évidemment – est caractérisé par un ensemble (en grisé sur la figure 1), qui a une intersection non vide avec chacun des trois sous-ensembles distingués.

III. LE DÉVELOPPEMENT
DE LA PROBABILITÉ SUBJECTIVE

On commencera par analyser la distinction « poppérienne » entre probabilité subjective et objective telle qu’elle s’exprime dans la Logique de la découverte scientifique, avant d’envisager le développement de la probabilité proprement subjective réalisé par Ramsey, de Finetti et plus près de nous, Savage.

OBJECTIVISME ET SUBJECTIVISTE

Il s’en faut de beaucoup que la distinction entre probabilités objective et subjective soit bien établie dès les débuts du calcul des probabilités – on s’en est expliqué dans l’introduction à cet article. Elle ne l’était même pas chez les plus grands probabilistes. Par exemple, Laplace (1825, p. 36-37) emploie les termes de « degré de croyance » ou de « degré de vraisemblance », alors même qu’il expose sa définition – classique – de la probabilité. Qui plus est, pour un déterministe tel que lui, la probabilité est une « mesure de notre ignorance » – une notion subjective s’il en est ! D’ailleurs, si les cas à considérer dans la fameuse définition sont également possibles, c’est tout simplement parce que nous – donc individuellement – ne voyons aucune raison de les distinguer : c’est le fameux « principe de l’absence de raison suffisante », déjà évoqué. On peut donc à bon droit soutenir que Laplace juxtapose les deux approches de la probabilité.

147

À vrai dire, c’est Popper qui doit être crédité d’avoir été le premier à systématiser la différenciation conceptuelle entre probabilités objective et subjective, lui donnant ainsi ses lettres de noblesse. Il faut cependant admettre que la distinction était dans l’air du temps, en ces années trente, particulièrement dramatiques et troublées, pleines de bruit et de fureur. Pour preuve de cette assertion, il suffira de citer Borel (1939, p. 70-71), affirmant bien fort « qu’il fallait insister (…) sur le caractère subjectif de la probabilité, caractère connu depuis fort longtemps (…) ».

Cela étant, dans sa Logik der Forschung, Popper (1934, 1980, p. 148 et sq.) distingue trois grandes interprétations possibles du concept : la première est subjectiviste et psychologiste aussi, en ce sens qu’elle « traite le degré de probabilité comme une mesure des sentiments de certitude ou d’incertitude, de croyance ou de doute, que peuvent faire naître en nous certaines assertions ou conjectures » ; la deuxième est l’interprétation keynésienne de la probabilité comme relation logique entre des énoncés, dont Popper dit qu’elle n’est qu’une variante de l’interprétation subjective, puisqu’elle s’appuie sur des « degrés de croyance rationnelle » – on a déjà abordé cette question supra dans cet article.

Enfin, il y a l’interprétation objective de la probabilité pour laquelle tout énoncé de probabilité numérique indique « la fréquence relative à laquelle un événement d’un certain type (…) se produit dans une suite d’occurrences ».

Notre auteur se range, pour sa part, dans le camp des « objectivistes », mais, comme on l’a vu en détails, il a tenté dans la Logik der Forschung de reconstruire la théorie de la probabilité comme une « théorie fréquentielle modifiée ».

Au total, la distinction entre les approches objective et subjective de la probabilité est non seulement commode, mais aussi éclairante. Le moment est maintenant venu d’examiner le développement de la branche subjectiviste.

LA PROBABILITÉ SUBJECTIVE :
DE RAMSEY ET DE DE FINETTI…

On peut toujours remonter dans le passé et trouver des précurseurs à toute idée. Pour ce qui concerne la probabilité subjective, le nom qui vient à l’esprit est celui de John Venn (1888), dont The Logic of Chance comporte un chapitre 6 consacré au « côté subjectif de la probabilité ». 148(Ce chapitre intitulé Degree of belief est partiellement reproduit dans l’ouvrage de Kyburg & Smokler (1964), ouvrage qui contient plusieurs textes essentiels émanant du courant subjectiviste.)

Toutefois, le véritable début de cette approche de la probabilité remonte à l’année 1926, date de la rédaction de Truth and Probability par Ramsey. (Cet essai de 1926 ne sera publié qu’après sa mort, soit en 1931).

Frank Plumpton Ramsey est donc décédé très jeune, à 26 ans. Il était un Fellow de Cambridge, où il côtoyait J.M. Keynes. Il s’intéressait tout spécialement aux problèmes de la logique mathématique. Il est également l’auteur de deux articles d’économie bien connus, dont le fameux : « A Mathematical Theory of Saving ».

Ramsey (1926, p. 56 et sq.) part d’une critique du degré de croyance keynésien pour construire une véritable « logique des croyances partielles ». Il rejette l’idée du premier, de la probabilité comme degré de connaissance logique. Il propose plutôt de mesurer ce degré par un coefficient ou quotient de pari (« betting quotient ») : le degré de croyance dans une proposition de la part d’un homme à un moment déterminé est mesuré par le taux pour lequel cet homme est prêt à parier que p est vraie. Autrement dit, une croyance de degré indique que l’homme en question est prêt à payer une proportion d’une unité de valeur, pas plus, pour avoir droit à une unité de valeur si p est vraie et à rien si est faux.

Par ailleurs, Ramsey avait bien vu que la détermination des degrés de croyance devait aller de pair avec l’estimation de l’utilité du coefficient de pari3 pour l’individu considéré. Par exemple, je peux parier 50 euros pour en recevoir 100, mais je ne serai certainement pas d’accord de parier 100 000 euros pour en recevoir 200 000. Autrement dit, l’utilité marginale de la monnaie n’est pas constante et ne peut être représentée par une fonction linéaire.

Le deuxième nom important à citer est celui de de Finetti (1937, p. 3), qui se définit lui-même comme un subjectiviste : « Le point de vue que j’ai l’honneur d’exposer ici peut être considéré comme la solution extrême du côté du subjectivisme ». Dans de Finetti (1973, p. x), il écrit d’ailleurs, en lettres capitales et de manière quelque peu provocatrice : « La probabilité n’existe pas. »

149

Quoi qu’il en soit, dans ses conférences à l’Institut Henri Poincaré, en 1937, notre auteur commence par définir une logique du probable. Il part en fait d’un ensemble d’axiomes qualitatifs au nombre de quatre : (A1) un événement incertain ne peut paraître que s’il est, soit aussi probable, soit plus probable, soit moins probable qu’un autre événement ; (A2) un événement incertain semble – ce terme est important d’un point de vue subjectiviste – toujours plus probable qu’un événement impossible et moins probable qu’un événement certain ; (A3) un axiome de transitivité ; (A4) les inégalités se conservent dans les sommes logiques : si E est un événement incompatible avec 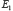et alors est plus probable, moins probable ou aussi probable que 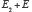si 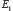est plus probable, moins probable ou aussi probable que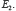

De Finetti (1937, p. 5 et sq.) montre alors en s’appuyant sur ce système d’axiomes, qu’il existe une mesure quantitative de la probabilité ainsi que de la probabilité conditionnelle – moyennant un axiome supplémentaire. Cependant, il relève que l’on peut également parvenir à une définition quantitative directe de la probabilité en précisant « l’idée banale et évidente que le degré de probabilité attribué par un individu à un événement donné est révélé dans les conditions dans lesquelles il serait disposé à parier sur cet événement ». De Finetti préfère in fine la seconde manière de procéder, rejoignant ainsi Ramsey.

Dès lors, si un individu évalue le prix pour lequel il serait prêt à accepter l’échange d’une somme quelconque S, subordonnée à l’occurrence d’un événement déterminé E, contre la somme S, alors on dira que est la mesure du degré de probabilité que cet individu attribue à E.

Cependant, lorsqu’une personne a évalué les probabilités d’un ensemble d’événements, deux cas peuvent se présenter : soit il est possible de parier sur elles en s’assurant de gagner à tous les coups, soit cette possibilité n’existe pas. Dans le premier cas, les probabilités évaluées par cette personne sont intrinsèquement contradictoires ; dans le second par contre, la personne en question est cohérente. De Finetti (1937, p. 7) conclut que « c’est précisément cette condition de cohérence qui constitue le seul principe d’où l’on puisse déduire tout le calcul des probabilités ».

150

… À SAVAGE

Venons-en à présent au troisième grand théoricien de la probabilité subjective : Jimmie Savage, auteur du livre The Foundations of Statistics, ouvrage qui a eu un très grand retentissement chez les statisticiens. (Savage parle, pour sa part, de « probabilité personnelle » plutôt que subjective, mais c’est une pure question de sémantique.)

Savage (1954b) propose en fait « une théorie du comportement cohérent en situation d’incertitude ». Plus précisément, soit un ensemble S d’états du monde avec leurs probabilités associées (subjectives bien sûr, donc obtenues par pari) et un ensemble F de conséquences. Une action est une application arbitraire de S dans F, associant une conséquence à chaque état du monde. On définit ensuite un préordre total sur l’ensemble des actions par la relation « n’est pas préféré à ». Ce préordre – la relation en question est réflexive et transitive – peut être représenté par une fonction numérique, l’utilité, unique à une transformation linéaire près, et qui permet d’associer un nombre U(f) à chaque conséquence 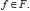L’individu choisira alors l’action qui maximise l’espérance mathématique – dans le sens où ce terme est habituellement utilisé en théorie des probabilités – de l’utilité. Plus formellement, pour toutes actions f et g de F, f est préférée à g si et seulement si

(5)

où l’utilité espérée de f est définie par

(6)

La définition en question est, bien entendu, similaire pour g – mutatis mutandis.

Si l’on substitue « somme de monnaie » à conséquence, on retrouve bien les idées essentielles de Ramsey. À cet égard, Savage (1954b, p. 279) écrit d’ailleurs explicitement que « les concepts de probabilité et d’utilité de Ramsey sont exactement les mêmes que ceux présentés dans ce livre », mais il ajoute, pour définir l’apport spécifique de ce dernier : « ses définitions de la probabilité et de l’utilité sont simultanées et interdépendantes ».

Subsiste néanmoins une question : comment rendre l’utilité numérique, autrement dit, comment déterminer la fonction U(.) dans (5) et (6) ? La réponse avait été donnée par Luce et Raiffa (1957, p. 304), dans 151un ouvrage qui fit époque : « la contribution de Savage (…) est une synthèse de l’approche de l’utilité de Von Neumann-Morgenstern à la prise de décision et du calcul de la probabilité subjective de de Finetti ». Donnons donc quelques précisions sur cette théorie de l’utilité.

Jusqu’à la parution de la Theory of Games and Economic Behavior (1944) de von Neumann-Morgenstern, les économistes partageaient la conception ordinale de l’utilité, initialement proposée par Pareto. L’apport des deux auteurs a été de « cardinaliser » l’utilité, un peu comme pour la température, c’est-à-dire moyennant fixation du zéro et de l’unité – en termes plus mathématiques, une telle mesure est définie à une application linéaire près, on l’a déjà précisé. Pour y parvenir, von Neumann et Morgenstern (1953, p. 18-19) introduisent les probabilités de la manière suivante. Considérons trois événements A, B et C tels que 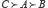et un nombre réel compris entre 0 et 1. Si l’événement certain A est exactement aussi « désirable » que l’évènement composé 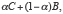alors la probabilité constitue une évaluation numérique du degré de préférence de A sur B rapporté au degré de préférence de C sur B. Telle est l’idée essentielle des deux auteurs, le reste est une question d’axiomatisation (voir sur ce point, von Neumann-Morgenstern (1953, appendix, p. 617-632). Précisons cependant que leur conception de la probabilité était objective, « une fréquence de long terme » (frequency in the long run) dans leurs propres mots.

Savage connaissait bien l’axiomatisation de von Neumann-Morgenstern et il avait d’ailleurs écrit, en collaboration avec Friedman, deux articles sur la question de l’utilité – voir Friedman et Savage (1948, 1952). Son apport propre a été de substituer les probabilités subjectives aux fréquences neumanniennes et d’insérer le tout dans une théorie du comportement de l’individu rationnel face au risque. (Précisons cependant qu’il n’admet pas la cardinalité de l’utilité ainsi définie, mais c’est un autre débat.)

CRITIQUES, DONT CELLE D’ALLAIS,
DE L’APPROCHE SUBJECTIVE

Voyons d’abord la version Ramsey-de Finetti de la probabilité subjective. Les objections qu’on peut lui adresser, ne portent pas sur sa logique interne : la théorie est cohérente et correcte d’un point de vue formel. Par contre, son application soulève au moins deux types de problèmes :

152

1. La probabilité subjective ne peut pas être confrontée à l’expérience, car comme le dit de Finetti (1937, p. 18), « un événement quelconque ne peut qu’arriver ou ne pas arriver, et ni dans un sens ni dans l’autre, on ne peut décider quel était le degré de doute avec lequel il était “raisonnable” ou “juste” de l’atteindre avant de savoir s’il était réalisé ou non. » C’est évidemment gênant d’un point de vue scientifique.

2. Une théorie subjective est impuissante à rendre compte de nombre d’observations du monde physique, notamment des régularités statistiques caractéristiques des phénomènes aléatoires telles qu’on peut les observer par exemple en mécanique statistique. (Rappelons la phrase, déjà citée, de de Finetti [1973] : la probabilité n’existe pas !)

En ce qui concerne la théorisation de Savage, il faut d’abord remarquer qu’elle ne fait pas l’unanimité chez les subjectivistes. De Finetti (1957, p. 7), en particulier, a émis à son encontre des réserves certaines :

J’hésite à suivre Savage dans cette direction (l’unification de la théorie de la probabilité et de l’utilité dans la théorie de la décision) ; ces concepts ont en effet, par rapport à ma manière de voir, des « valeurs » différentes : une valeur indiscutable dans le cas de la probabilité, une valeur assez incertaine dans le cas de l’utilité et des conditions de rationalité pour un comportement en situation de risque.

En termes voilés, mais néanmoins suffisamment clairs, de Finetti doute donc de la valeur du critère de maximisation de l’utilité espérée comme règle comportementale rationnelle en incertitude. Sans doute aussi lui préfère-t-il le critère plus simple de l’espérance de gain monétaire.

Maurice Allais, dans son grand article de 1953 publié, en français, dans Econometrica, s’en prend rien moins qu’à « l’école américaine » dans son ensemble, par quoi Allais (1953a, p. 516 n.21) entend Baumol, de Finetti, Friedman, Marschak, von Neumann-Morgenstern, Samuelson et Savage. Cette liste comporte aussi bien des subjectivistes que des objectivistes.

Bien évidemment, on se concentrera ici sur la seule critique des thèses de L. J. Savage et non sur celles de l’école américaine en général. De ce point de vue, il faut signaler qu’Allais (1953a) ne pouvait avoir connaissance du livre de Savage qui parut l’année suivante ; par contre, il disposait de la communication – un résumé en réalité des Foundations… – présentée par ce dernier lors du Colloque international sur le risque, tenu à Paris, du 12 153au 17 mai 1952 ; celle-ci a ensuite été publiée dans CNRS (1954). Sur le Colloque de Paris, sur son importance et plus généralement, sur le « paradoxe d’Allais », Mongin (2014) fournit toutes les précisions souhaitables.

Allais reproche d’abord à Savage de ne donner aucune définition de la rationalité, si ce n’est une pseudo-définition, tautologique, du type : est rationnel tout qui se conforme aux axiomes retenus. Aussi notre auteur présente-t-il la sienne, qu’il qualifie d’abstraite et qui se résume en la formule suivante : « un homme est réputé rationnel lorsque (a) il poursuit des fins cohérentes avec elles-mêmes, (b) il emploie des moyens appropriés aux fins poursuivies », Allais (1953a, p. 518). Il suit, notamment, de cette définition qu’un individu rationnel préfèrera toujours une perspective aléatoire procurant des gains constamment supérieurs à ceux d’une autre perspective aléatoire et que seules les probabilités objectives définies par rapport aux fréquences observées doivent être prises en considération.

La critique allaisienne est double : il s’agit de montrer, d’une part, que la définition – abstraite – de la rationalité conduit à un comportement, parfois en opposition avec le principe de Bernoulli ; d’autre part, qu’expérimentalement, certaines formes de comportement rationnel sont contradictoires avec ledit principe.

On passera rapidement sur le premier volet de la critique en renvoyant à Allais (1953a, p. 522-524). La seconde approche – fondée sur l’observation du comportement d’un homme réputé rationnel – recevra, par contre, toute l’attention qu’elle mérite.

De ce point de vue, la critique d’Allais porte tout spécialement sur l’axiome 5 de Savage (1954a, p. 32), axiome qu’il qualifie « d’indépendance » et dont il est commode d’expliquer la signification à partir du schéma suivant :

Fig. 2

154

Sur cette figure 2, sont représentées deux perspectives aléatoires, numérotées 1 et 2, qui ont une partie commune. L’axiome 5 de Savage revient à dire que la relation de préférence entre les deux perspectives n’est pas modifiée en cas de déplacement quelconque de cette partie commune.

Pour Allais (1953a, p. 525), de nombreux exemples de comportements rationnels contredisent l’axiome de Savage. Voici l’un d’entre eux4 :

Situation A 100 000€ avec probabilité 1	E(A) = 100 000	Situation C 100 000€ avec probabilité 0,11 0€ avec probabilité 0,89	E(C) = 11 000
Situation B 500 000€ avec probabilité 0,1 100 000€ avec probabilité 0,89 0€ avec probabilité 0,01	E(B) = 139 000	Situation D 500 000€ avec probabilité 0,1 0€ avec probabilité 0,9	E(D) = 50 000

In fine, Allais [1953a, p. 527] concluait des réponses reçues que « pour la plupart des gens très prudents (…) et très rationnels », ces réponses étaient de la forme :

Or, si un individu i préfère A à B, alors, en vertu de l’axiome d’indépendance de Savage, il devrait aussi préférer C à D, ce qui est, répétons-le, contradictoire avec les données observées à l’issue de l’enquête.

Ce contre-exemple a reçu le nom de « paradoxe d’Allais ». Il a été reproduit à de multiples reprises tout en donnant à chaque fois des résultats similaires5. De ces expériences répétées, il suit la conclusion 155ultime que la théorisation de Savage ne représente pas un modèle descriptif adéquat du comportement de l’individu rationnel en incertitude. Par ricochet, la probabilité subjective elle-même se trouve mise à mal par cette inadéquation empirique notoire du modèle. On dira : le jugement est sévère. Pas tant que cela, si l’on veut bien ne pas oublier que Friedman et Savage (1952, p. 473) avaient eux-mêmes écrits que l’hypothèse de l’utilité espérée « devrait être rejetée si ses prévisions étaient, le plus souvent, contredites par l’observation ».

IV. LA RÉVOLUTION DE L’AXIOMATISATION

On développera d’abord l’axiomatisation de la théorie opérée par A.N. Kolmogorov, avant de souligner qu’elle s’inscrit dans un cadre objectiviste. Pour terminer, on s’attardera sur l’interprétation poppérienne – le second Popper en quelque sorte ! – de la probabilité en tant que propension.

ET KOLMOGOROV VINT…

Durant tout le xixe siècle, la théorie des probabilités n’était pas considérée comme une branche des mathématiques, mais plutôt de la physique. En réalité, l’axiomatisation de la probabilité était dépendante des progrès de la théorie de l’intégrale. De ce point de vue, les dates importantes sont celles des publications de Cauchy (1823) et de Riemann (1867). Cependant, l’étape décisive sera effectuée par Lebesgue avec l’intégrale qui porte son nom. Pour voir de quoi il s’agit, prenons l’exemple d’une variable aléatoire X uniformément distribuée sur 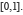On sait que dans ce cas, pour 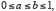on a :

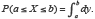
Si A est une partie de 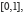le calcul de la probabilité 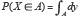est équivalent à la recherche de la mesure de A (sa longueur). C’est le mérite de Lebesgue d’avoir résolu ce problème en 1901.

Dès ce moment, il était techniquement possible de traiter les situations où il y avait une infinité (dénombrable ou pas) de cas possibles – si l’on 156reprend la définition classique de la probabilité – et donc d’axiomatiser la théorie des probabilités. La première tentative dans ce sens fut celle de von Mises (1919), mais comme on l’a vu, elle n’était pas vraiment satisfaisante. Par contre, la seconde, chronologiquement parlant, celle opérée par Kolmogorov en 1933, a révolutionné la théorie et a fini par s’imposer durablement.

Sans entrer dans trop de détails, tentons de donner brièvement l’essentiel de l’apport du mathématicien russe et considérons à cet effet une expérience aléatoire Ɛ, dont les résultats élémentaires, notés sont en nombre n. Soit alors l’ensemble Un événement n’est rien d’autre qu’un sous-ensemble de 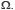Notons 𝓟(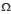) l’ensemble de tous les événements, c’est-à-dire des parties de 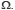𝓟(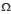) est une algèbre d’événements, ce qui signifie que cette famille d’événements comprend l’ensemble vide et est stable pour les opérations de complémentation et de réunion finie. On appelle alors mesure de probabilité sur (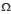, 𝓟(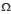)) toute application P telle que :

1. Pour tout événement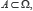

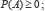
2. 𝓟(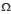) = 1 ;

3. Si A et B sont deux événements incompatibles de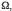

L’étape suivante consiste à envisager des univers de résultats dénombrables et non plus finis, Kolmogorov (1933, p. 14) introduit en conséquence un axiome supplémentaire de continuité dénombrable : si est une suite décroissante d’événements de
𝓟(), d’intersection vide, alors

L’algèbre de tous les événements devient à présent une tribu, c’est-à-dire une famille d’événements contenant l’événement impossible et stable pour les opérations de complémentation et de réunion dénombrable. Il s’ensuit qu’il faut alors modifier le point 3 dans la définition de l’application P et le remplacer par

4. pour toute famille dénombrable d’événements incompatibles,

157

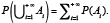
Dernière étape : considérer des univers de résultats infinis-continus. Dans ce cas, l’ensemble de tous les événements est trop vaste et on s’intéresse en conséquence à une tribu particulière, appelée tribu des boréliens de ℝ.

Notons 𝓑0 la tribu des sous-ensembles de ℝ qui sont des unions finies d’intervalles disjoints de la forme 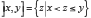et 𝓑 = (𝓑0) la plus petite tribu engendrée par 𝓑0. La tribu engendrée est précisément celle des boréliens de ℝ.

On a finalement le résultat suivant appelé théorème du prolongement des mesures de probabilité (cité d’après Bismans [2016, p. 84] en simplifiant légèrement) :

Toute mesure de probabilité 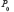définie sur une algèbre 𝓑0 d’événements de 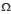= ℝ admet un prolongement unique en une mesure de probabilité, notée P, définie sur la tribu (𝓑0) engendrée par 𝓑0.

Ce théorème signifie que si une probabilité 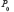est attribuée à un sous-intervalle de l’algèbre 𝓑0, alors la même probabilité sera attribuée à cet événement par référence à 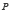définie sur la tribu des boréliens 𝓑 =  (𝓑0).

Avec un tel formalisme, l’introduction de la probabilité et de l’espérance conditionnelles est aisée et naturelle. Kolmogorov (1933) définit l’une et l’autre dès le chapitre 1 pour des variables aléatoires revêtant un nombre fini de valeurs, avant de généraliser les deux concepts à des variables aléatoires absolument continues – ce qui fait l’objet du chapitre 5.

Tous ces développements peuvent paraître passablement abstraits. En réalité, Kolmogorov (1933, p. 3) a pris soin d’écrire un paragraphe entier – le numéro 2, la monographie étant subdivisée en paragraphes –, qui est consacré à la relation de sa théorie avec les « données expérimentales ». Indubitablement donc, Kolmogorov se range dans le camp des objectivistes, même s’il est possible bien sûr de donner une interprétation alternative – subjective en l’occurrence – de son axiomatique.

158

L’INTERPRÉTATION PROPENSIONNISTE

On a déjà signalé que Popper avait abandonné l’interprétation fréquentiste qu’il défendait encore dans la Logique de la découverte scientifique et qu’il lui préférait désormais une approche en termes de propensions. Cette nouvelle interprétation fut exposée pour la première fois dans Popper (1963, 1985, chapter 1, p. 59 et sq.).

Ce changement, car c’en est un, Popper (1983, p. 360) le voit comme une conséquence de l’évolution de la théorie mathématique des probabilités – qu’il appelle la théorie néoclassique. Dans ses propres termes : « le passage de l’interprétation fréquentiste à l’interprétation propensionniste correspond au passage de la théorie mathématique des fréquences (…) au traitement néo-classique de la probabilité en termes de théorie de la mesure ». Autrement dit, le « second Popper » se situe explicitement dans le sillage de Kolmogorov et de l’axiomatisation de la probabilité développée par ce dernier.

Popper (1983) développe plusieurs éléments qui montrent la supériorité de la théorie axiomatisée sur les mathématiques fréquentistes :

1. la probabilité est une application (mathématique) jouissant de propriétés déterminées ; il n’est donc plus nécessaire de définir le concept en tant que tel ;

2. les distributions uniformes ne sont qu’un exemple parmi un ensemble très vaste de lois de probabilité ;

3. elle produit, via la convergence presque sûre, des théorèmes qui affirment qu’une suite aléatoire converge vers sa fréquence asymptotique avec une probabilité égale à un – ce sont les lois fortes des grands nombres.

Au total, il n’y a donc pas un formalisme qui serait propre à l’approche propensionniste. Au contraire, cette dernière se situe explicitement dans le prolongement direct de la théorie axiomatisée.

Avant de donner une définition formelle de la probabilité-propension, prenons deux exemples, l’un économique, l’autre purement statistique qui permettront d’éclairer sa signification et faciliteront sa compréhension.

Keynes dans sa General Theory a introduit le concept de propension à consommer, qu’il définit comme une fonction mathématique « assez 159stable » – comprenons qu’elle subit des variations minimes que l’on peut considérer comme aléatoires. Keynes (1936, p. 90-91) écrit par ailleurs que « le montant que la communauté dépense en consommation dépend évidemment : 1) en partie du montant de son revenu ; 2) en partie des autres circonstances objectives déterminant ce revenu ; 3) en partie des besoins subjectifs, des dispositions psychologiques et des habitudes des individus qui la composent, de même que des principes qui gouvernent la répartition du revenu entre ces individus ». Ce que notre auteur dit dans ce passage – sans faire référence à Popper bien évidemment –, c’est que la propension à consommer est en fait une quantité aléatoire qui dépend d’un ensemble de facteurs objectifs et subjectifs, qu’elle est donc le produit d’une situation donnée dans toute sa complexité.

Autre exemple, développé cette fois dans Popper (1990) : celui des probabilités de survie consignées dans les tables de mortalité qu’utilisent notamment les compagnies d’assurance. Si l’on s’interroge sur leur signification, on répondra naturellement que la probabilité de survie d’un individu est une propriété de l’état de santé de cet individu. La réponse est correcte, mais insuffisante. Par exemple, cette probabilité est affectée par les progrès de la médecine : en effet, la mise au point de nouveaux médicaments – des antibiotiques par exemple – va modifier les probabilités de survie de chaque individu, qu’il tombe ou non malade. Cependant, il est indispensable d’aller encore plus loin et de considérer que le nouveau médicament, du moins lors de son lancement, est coûteux et qu’il pourrait bien ne pas être acquis par tout un chacun, même s’il existe un système de sécurité sociale organisé. Comme le dit avec humour Popper, il faut donc également prendre en compte la variable « état de santé du portefeuille » des individus pour déterminer leurs probabilités de survie.

La conclusion à tirer de ce dernier exemple est simple : les probabilités de survie dépendent de la situation complexe donnée et non du seul état de santé physique des individus considérés.

Pour Popper, les probabilités mesurent la propension d’un événement – nécessairement lié à un phénomène aléatoire – à se produire sur une échelle additive où le nombre 1 mesure la propension de l’événement certain, compte tenu d’une situation déterminée. Dans cette optique, les lois des grands nombres constituent le « raccord », le pont, entre la probabilité 160théorique et la notion empirique de fréquence, mais la probabilité n’est en aucun cas une fréquence relative.

Il s’agit là d’une interprétation objective de la probabilité, car les propensions sont des propriétés d’un dispositif expérimental, d’une situation à chaque fois spécifique. C’est pourquoi Popper (1982a, 1983) parle aussi d’une « théorie physique des propensions ». Il va même plus loin, puisque, pour lui, la propension est une réalité physique au même titre que les forces d’attraction ou de répulsion.

Il n’est pas difficile de formaliser la conception propensionniste en utilisant les outils mathématiques de la théorie des probabilités. Popper (1983, p. 283-284) propose d’ailleurs un exemple d’une telle formalisation, que l’on va cependant adapter à un cadre kolmogorovien strict.

Soit l’espace de probabilité (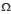, 𝓐, P), où 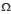est l’univers des résultats d’une expérience aléatoire, 𝓐 est une tribu d’événements et P une mesure de probabilité. Si A ∈ 𝓐 et si S décrit l’ensemble des conditions situationnelles de l’expérience ou du phénomène aléatoire, alors

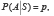
ce qui signifie que la probabilité conditionnelle de l’événement A étant donnée (ou sachant) la situation S, est égale à la propension p.

Il suit que les propensions sont donc des probabilités conditionnelles – concept parfaitement intégré dans l’axiomatisation de Kolmogorov, on l’a vu – et non de simples probabilités – absolues pourrait-on dire – de la forme C’est sans doute cette proximité conceptuelle qui permet à Popper (1983, p. 374) d’écrire que la théorie néoclassique « favorise l’interprétation propensionniste des probabilités ».

L’interprétation de Popper a le mérite, entre autres, de traiter le cas des événements singuliers ou isolés, non répétitifs, puisque, par définition, elle n’est nullement fondée sur la notion de fréquence relative. (Pour une comparaison entre propensionnisme et fréquentisme, on renverra à Popper [1983, p. 286].) Certes, le concept de propension ou de disposition est moins usité dans les sciences dures que dans les sciences de l’homme. Il n’empêche qu’il est tout aussi fécond dans les premières que dans les secondes.

L’apport de l’auteur ne se situe donc pas sur un plan mathématique. Il fait à cet égard pleinement sien le formalisme kolmogorovien. Il est bien plutôt d’avoir montré que la conception propensionniste, arcboutée 161sur cette axiomatique, est celle – et de loin – qui est la plus appropriée à la recherche en physique moderne. En témoigne le fait que Popper (1982b) consacre la totalité du tome III de son Postscript à la seule étude de la « théorie des quanta et le schisme en physique ».

V. DÉTERMINISME ET PROBABILITÉ OBJECTIVE

De Laplace à Popper, tel était le parcours, le cheminement que nous voulions retracer. La boucle est donc bouclée, pourrait-on dire. Oui, mais en partie seulement, pas totalement, car il reste qu’entre les deux auteurs, la différence n’est pas que d’époque ou chronologique ; elle est aussi conceptuelle, dans la mesure où l’interprétation poppérienne de la probabilité est indissolublement liée à une critique du déterminisme laplacien. Mieux : la seconde est la condition de la première. Expliquons-nous.

Dans une page célèbre de son Essai…, Laplace (1825, p. 32-33) a parfaitement décrit son programme de recherche déterministe :

Tous les événements, ceux mêmes qui par leur petitesse semblent ne pas tenir aux grandes lois de la nature, en sont une suite aussi nécessaire que les révolutions du soleil. Dans l’ignorance des liens qui les unissent au système entier de l’univers, on les a fait dépendre des causes finales ou du hasard (…) Les événements actuels ont avec les précédents une liaison fondée sur le principe évident, qu’une chose ne peut pas commencer d’être, sans une cause qui la produise. (…) Nous devons donc envisager l’état présent de l’univers comme l’effet de son état antérieur, et comme la cause de celui qui va suivre. Une intelligence qui pour un instant donné, connaîtrait toutes les forces dont la nature est animée et la situation respective des êtres qui la composent (…) embrasserait dans la même formule les mouvements des plus grands corps de l’univers et ceux du plus léger atome : rien ne serait incertain pour elle, et l’avenir comme le passé serait présent à ses yeux.

L’intelligence à laquelle se réfère ce texte n’est pas celle d’un dieu, d’un « démon » ou d’une divinité quelconque. Selon l’heureuse expression de Popper, il s’agit bel et bien d’un « super-scientifique », qui se comporte en savant, armé des lois de la dynamique classique et capable d’embrasser la totalité de l’univers dans son devenir.

162

Ce super-scientifique – c’est sa première caractéristique – dispose de la capacité de prévoir le futur, qui n’est rien d’autre que l’effet de l’état présent de l’univers. De plus, précision capitale, il est en mesure de prévoir quantitativement, c’est-à-dire mathématiquement, l’état du système du monde à n’importe quel instant du futur. On peut donc, dans ce cas, parler à bon droit de prédictibilité parfaite de l’avenir, moyennant bien sûr la connaissance du passé et des conditions initiales du mouvement.

Seconde caractéristique, le super-scientifique a pour tâche d’éliminer le hasard, l’incertitude en les remplaçant par l’explication causale. L’aléatoire n’existe pas vraiment ; il n’est que l’expression de notre ignorance mesurée par la probabilité. C’est déjà dit dans le texte cité. Mais Laplace (1825, p. 223) est encore plus explicite sur le sujet lorsqu’il écrit : « (…) le hasard n’a donc aucune réalité en lui-même : ce n’est qu’un terme propre à désigner notre ignorance sur la manière dont les différentes parties d’un phénomène se coordonnent entre elles et avec le reste de la Nature ».

Prédictibilité du futur et élimination de l’aléatoire constituent donc la matrice du déterminisme scientifique que Popper (1982a, p. 31) définit comme suit : « La structure du monde est telle que tout événement peut être rationnellement prédit, au degré de précision voulu, à condition qu’une description suffisamment précise des événements passés, ainsi que toutes les lois de la nature nous soient données. »

On peut bien entendu émettre nombre de critiques à l’égard de cette forme de déterminisme6. Par exemple, comment un calcul de notre ignorance – la probabilité – peut-il être vérifié par des faits physiques ? Ou encore, on peut lui objecter qu’une bonne partie de la physique contemporaine – notamment celle qui est fondée sur la théorie des quanta – n’a de sens qu’interprétée en termes probabilistes.

Popper va plus loin dans le questionnement. Le cœur de sa critique réside dans le fait qu’un scientifique ne peut prédire, rationnellement, les résultats produits par la croissance de nos connaissances. Dès lors, aucun système physique n’est totalement prédictible.

Les étapes essentielles du raisonnement de Popper (1982a, p. 58-65) sont les suivantes :

163

(i) le déroulement de l’avenir – prédictible pour un déterministe – dépend, dans une large mesure, de l’accroissement de nos connaissances scientifiques (une proposition jugée tout à fait raisonnable par Popper) ;

(ii) l’auto-prédiction des connaissances scientifiques est impossible et ceci est vrai pour n’importe quel ensemble de prédicteurs ;

(iii) la croissance de nos connaissances ne peut donc être prédite.

In fine, il s’ensuit que la vision d’un monde strictement déterminé n’est pas tenable sur un plan scientifique et qu’il faut donc lui substituer celle d’un univers « ouvert », « irrésolu », indéterminé, dans lequel le hasard et l’aléatoire occupent une place centrale. C’est l’indéterminisme de Popper.

Il faut alors en tirer le grand enseignement que la critique poppérienne du déterminisme défendu par Laplace et corrélativement, de sa conception de la probabilité comme mesure de notre ignorance, induit une rupture théorique significative.

À l’univers laplacien, déterminé de part en part, dans lequel le hasard n’est qu’un reliquat de l’insuffisance de nos connaissances scientifiques, fait place un univers ouvert, indéterminé par nature et par principe, constitué de propensions physiques qui trouvent à se réaliser ou non – bref à advenir.

Tel est, en définitive, le grand mérite de Popper : avoir, dans un même mouvement, critiqué, jusque dans ses fondements, le déterminisme scientifique et sa probabilité-ignorance, tout en y substituant un univers de propensions, régi par la multitude et le choc des probabilités conditionnelles, qui s’entrecroisent et s’interfèrent. À vrai dire, le mérite n’est pas mince. Nous disposons désormais d’une interprétation objective, mathématiquement axiomatisée, de la probabilité, opérationnelle à tous égards.

Que demander de plus ? La boucle est à présent véritablement bouclée : Popper contre Laplace en somme.

164

CONCLUSIONS

Cet article a retracé l’évolution du concept mathématique de probabilité de Laplace à Popper, c’est-à-dire de la définition classique – nombre de cas favorables rapporté au nombre de cas possibles, ces derniers étant réputés également possibles – à la conception de la probabilité en tant que propension conditionnelle.

Bien entendu, un tel développement n’a rien de linéaire. Il est scandé par des ruptures, conceptuelles (objectivistes versus subjectivistes) autant que mathématiques. À cet égard, l’axiomatisation de la théorie des probabilités par Kolmogorov s’apparente à un véritable point de non-retour, même si elle est susceptible de recevoir diverses interprétations.

Trancher entre l’une ou l’autre de ces interprétations n’aurait pas grand sens. Elles ont toutes, à des degrés divers cependant, des points forts et des faiblesses, parfois marquées. Néanmoins, la conception du « dernier Popper » de la probabilité-propension, arcboutée à l’axiomatique de Kolmogorov, offre l’avantage de fournir une interprétation « objective » de la probabilité, débarrassée des limitations et des insuffisances de la conception fréquentiste traditionnelle.

Qui plus est, l’avancée interprétative de Popper se double d’une critique du déterminisme laplacien et de sa conception de la probabilité comme mesure de notre ignorance. De ce fait, univers indéterminé et probabilité-propension se conjuguent pour donner une grille théorique apte à mieux appréhender tant le monde physique que les sociétés.

Un débouché naturel de ce travail consisterait à reprendre la « diachronie » de la probabilité mathématique et à l’examiner en parallèle avec la question du déterminisme philosophique. Un vaste domaine qui, de Laplace à Thom, a fait l’objet de débats aussi intéressants que passionnés !

165

RÉFÉRENCES BIBLIOGRAPHIQUES

Allais, Maurice [1943], Traité d’économie pure, 3e édition, Paris, Éditions Clément Juglar, 1994.

Allais, Maurice [1953a], « Le comportement de l’homme rationnel devant le risque : critique des postulats et axiomes de l’école américaine », Econometrica, 21, p. 503-546.

Allais, Maurice [1953b], « La psychologie de l’homme rationnel devant le risque : la théorie et l’expérience », Journal de la Société Statistique de Paris, 94, p. 47-73.

Allais, Maurice [1979], « The So-Called Allais’ Paradox and Rational Decisions under Uncertainty », in Allais, Maurice & Hagen, Ole (éd.) [1979], Expected Utility Hypothesis and the Allais’Paradox. Contemporary Discussions of Decisions under Uncertainty with Allais’Rejoinder, Dordrecht, Reidel Publishing Company, p. 434-698.

Bismans, Francis [2016], Probabilités et statistique inférentielle. Prélude à l’économétrie, Paris, Ellipses.

Borel, Émile [1924], « À propos d’un traité de probabilités », Revue philosophique, No 98, p. 321-336, in Borel, Émile [1939], p. 134-146.

Borel, Émile [1939], Valeur pratique et philosophie des probabilités. Réédition en fac-simile, Paris, Jacques Gabay, 2009.

Breny, Henri [1975], Petit traité élémentaire de théorie des probabilités, 2e édition, Liège, Edibon.

CNRS [1954], Fondements et applications de la théorie du risque en économétrie, Paris, Éditions du Centre National de la Recherche Scientifique.

Cournot, Augustin A. [1851], Essai sur les fondements de nos connaissances et sur les caractères de la critique philosophique, in Cournot, Augustin A. [1975], Œuvres complètes, tome II, Paris, Vrin.

Daston, Lorraine J. [1988], Classical Probability and the Enlightenment, Princeton, Princeton University Press.

Finetti, Bruno de [1937], « La prévision : ses lois logiques, ses sources subjectives », Annales de l’Institut Henri Poincaré, tome 7, No 1, p. 1-68.

Finetti, Bruno de [1957], « L’informazione, il ragionamento, l’inconscio nei rapporti con la previsione », L’industria, No 2, p. 3-27.

Finetti, Bruno de [1975], Theory of Probability, vol. 2, Chichester, Wiley.

Finetti, Bruno de [1985], « Cambridge Probability Theorists », The Manchester School of Economic and Social Studies, No 53, p. 348-363.

166

Friedman, Milton & Savage, Leonard J. [1948], « The Utility Analysis of Choices Involving Risk », Journal of Political Economy, No 56, p. 279-304.

Friedman, Milton & Savage, Leonard J. [1952], « The Expected-Utility Hypothesis and the Measurability of Utility », Journal of Political Economy, No 60, p. 463-474.

Hacking, Ian [1975], The Emergence of Probability, Cambridge, Cambridge University Press.

Hicks, John R. [1979], Causality in Economics, Oxford, Basil Blackwell.

Jeffreys, Harold [1939], Theory of Probability, 2nd edition, Oxford, Clarendon Press, 1948.

Kahneman, Daniel & Tversky, Amos [1979], « Prospect Theory: An Analysis of Decision under Risk », Econometrica, No 47, p. 263-292.

Keynes, John M. [1921], A Treatise on Probability, in Collected Writings of John Maynard Keynes, tome 8, London-Cambridge, Macmillan-Cambridge University Press, 1973.

Keynes, John M. [1936], The General Theory of Employment, Interest and Money, in Collected Writings of John Maynard Keynes, tome 7, London-Cambridge, Macmillan-Cambridge University Press, 1973.

Keynes, John M. [1937], « The General Theory of Employment », Quarterly Journal of Economics, Vol. 51, No 2, p. 209-223. Repris dans Collected Writings of John Maynard Keynes, tome 14, London-Cambridge, Macmillan-Cambridge University Press, 1973.

Kolmogorov, Andreï N. [1933], Grundbegriffe der Wahrscheinlichkeitrechnung, Berlin, Springer. (Traduction anglaise : Foundations of the Theory of Probability, 2e édition, Rhode Island, AMS Chelsea Publishing, 2000.)

Krüger, Lorenz, Daston, Lorraine J. & Heidelberger, Michael (dir.), [1987], The Probabilistic Revolution, volume I: Ideas in History, Cambridge-London, A Bradford Book, The MIT Press.

Kyburg, Henry E. & Smokler, Howard E. (dir.) [1964], Studies in Subjective Probability, New York-London-Sidney, John Willey.

Laplace, Pierre-Simon [1814], Théorie analytique des probabilités, 2e édition, Paris, Courcier. (Disponible sur Internet).

Laplace, Pierre-Simon [1825], Essai philosophique sur les probabilités, 5e édition, Paris, Christian Bourgois, 1986.

Luce, Duncan R. & Raiffa, Howard [1957], Games and Decision. Introduction and Critical Survey, New York-London-Sydney, John Wiley & Sons.

Mises, Richard von [1919], « Grundlagen der Wahrscheinlichkeitsrechnung », Mathematische Zeitschrift, No 5, p. 52-99.

Mises, Richard von [1957], Probability, Statistics and Truth, second revised English edition, New York, Dover, 1981.

167

Mongin, Philippe [2014], « Le paradoxe d’Allais. Comment lui rendre sa signification perdue ? », Revue économique, No 65, p. 743-779.

Neumann, John von & Morgenstern, Oskar [1953], Theory of Games and Economic Behavior, third edition, Princeton, Princeton University Press.

Pascal, Blaise [1665], Traité du triangle arithmétique : avec quelques autres petits traités sur la même matière, Paris, Guillaume Desprez, in pascal, Blaise [1963], Œuvres complètes, Paris, Seuil.

Popper, Karl R. [1934], Logik der Forschung, Wien, Julius Springer.

Popper, Karl R. [1959], The Logic of Scientific Discovery, second English edition, London, Unwin Hyman, 1980.

Popper, Karl R. [1973], La logique de la découverte scientifique. Traduction de Nicole Thyssen-Rutten & Philippe Devaux, Préface de Jacques Monod, Paris, Payot.

Popper, Karl R. [1982a], Postscript to the Logic of Scientific Discovery. II. The Open Universe. An Argument for Indeterminism, London-New York, Routledge (Trad. française, L’univers irrésolu. Plaidoyer pour l’indéterminisme, Paris, Hermann, 1984.)

Popper, Karl R. [1982b], Postscript to the Logic of Scientific Discovery. III. Quantum Theory and the Schism in Physics, London-New York, Routledge, 1992.

Popper, Karl R. [1983], Postscript to the Logic of Scientific Discovery. I. Realism and the Aim of Science, London-New York, Routledge, 1992.

Popper, Karl R. [1989], Conjectures and Refutations. The Growth of Scientific Knowledge, fifth edition, London-New York, Routledge.

Popper, Karl R. [1990], A World of Propensities, Bristol, Thoemmes Press.

Ramsey, Frank P. [1926], « Truth and Probability », in Ramsey, Frank P. [1990], Philosophical Papers, Cambridge, Cambridge University Press.

Reichenbach, Hans [1935], Wahrscheinlichkeitslehre, Leiden, Sijthoff.

Reichenbach, Hans [1937], « Les fondements logiques du calcul des probabilités », Annales de l’Institut Henri Poincaré, No 7, fasc. 5, p. 267-348.

Savage, Leonard J. [1954b], The Foundations of Statistics, New York, Wiley.

Savage, Leonard J. [1961], « The Foundations of Statistics Reconsidered », Proceedings of the Fourth Berkeley Symposium on Mathematics and Probability, Berkeley, University of California Press. Reproduit dans kyburg, Henry E. & Smokler, Howard E. (dir.), [1964], p. 174-188.

Savage, Leonard J. [1951], « The Theory of Statistical Decision », Journal of the American Statistical Association, No 46, p. 55-67.

Savage, Leonard J. [1954a], « Une axiomatisation du comportement raisonnable face à l’incertitude », in CNRS [1954], p. 29-33.

Schneider, Ivo [1987], « Laplace and Thereafter: The Status of Probability Calculus in the Nineteenth Century », in Krüger, Lorenz, Daston, Lorraine J. & Heidelberger, Michael (dir.), [1987], p. 191-214.

168

Stigler, Stephen M. [1986], The History of Statistics. The Measurement of Uncertainty before 1900, Cambridge-London, The Belknap Press of Harvard University Press.

Szafarz, Ariane [1984], « Richard von Mises : l’échec d’une axiomatique », Dialectica, 38, p. 311-317.

Szafarz, Ariane [1985], « L’évolution du concept de probabilité mathématique de Pascal à Laplace », Technologia, 8 (3), p. 67-76.

Venn, John [1888], The Logic of Chance, third edition, re-written and enlarged, London-New York, Macmillan and co.